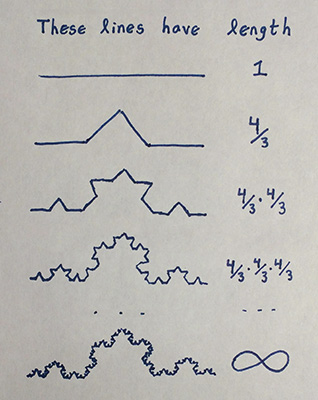The curve on the bottom is known as a Koch curve. It has infinite length! It is an example of a fractal, and it can be built by the following process. Start with a line segment. Replace the middle third of the line segment with two equal-length line segments in the shape of an equilateral triangle. Now repeat this process infinitely many times. At each iteration, the length of the total curve gets multiplied by 4/3. If 4/3 is multiplied by itself infinitely many times, the result is infinity. Hence, the length of the Koch curve is infinite.