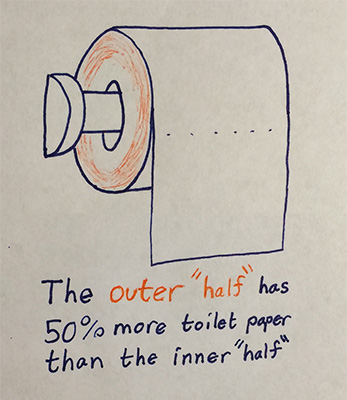
You've probably heard the expression that "Life is like a roll of toilet paper. The closer it gets to the end, the faster it goes." This leads us to a mathematical question: is there more toilet paper in the outer "half" (the region sketched in orange)? Surprisingly, the answer is yes. If there is a thickness of one inch of toilet paper, then the half-inch closer to the center contains less toilet paper than the half-inch further from the center.

How much more toilet paper is in the outer "half"? The answer depends on how big the roll of toilet paper is. Specifically, it depends on the ratio of the outer radius to the inner radius. If that ratio is 7/3, then there is 50% more volume in the outer cylindrical shell (shaded orange) than in the inner cylindrical shell. You can show this by using the formula for the area of a circle. For an extra challenge, determine what happens as the outer radius becomes really large. That is, for a really really large roll, how much more toilet paper is in the outer "half"?